 Впервые на русском языке в монографии «Геометрическая морфометрия: от теории к практике» обобщены традиционные и новейшие методы геометрической морфометрии и предложен новый подход – фенограмметрия, позволяющий применять методы геометрической морфометрии для анализа качественных признаков. Этот подход расширяет возможности для решения задач популяционной феногенетики, фенетики, таксономии и экологии
Впервые на русском языке в монографии «Геометрическая морфометрия: от теории к практике» обобщены традиционные и новейшие методы геометрической морфометрии и предложен новый подход – фенограмметрия, позволяющий применять методы геометрической морфометрии для анализа качественных признаков. Этот подход расширяет возможности для решения задач популяционной феногенетики, фенетики, таксономии и экологии
Геометрическая морфометрия (ГМ) как область биометрических исследований, позволяющая независимо анализировать изменчивость формы и размеров объектов возникла в конце 80-х годов XX в. и в настоящее время имеет достаточно широкое распространение за рубежом. Отсутствие монографического описания методов и технологий ГМ на русском языке ограничивало и затрудняло их использование российскими учеными. Публикация данной монографии во многом решает эту проблему, поскольку в книге изложены не только теоретические аспекты современной ГМ, но и даны детальные описания работы с основными свободно распространяемыми компьютерными программами. Впервые изложен авторский подход к анализу неметрических признаков с применением методов ГМ (фенограмметрия). Применение данного подхода раскрывает новые возможности для фенетики популяций (Тимофеев-Ресовский, Яблоков, 1973; Тимофеев-Ресовский и др., 1973; Яблоков, 1980; Яблоков, Ларина, 1985; Васильев, 1988, 2005; Васильев, Васильева, 2009).
Фенограмметрия основана на хорошо известном в популяционной генетике методе полигонов А.С. Серебровского (1970), предложенном им для сравнений популяций по частотам встречаемости аллелей разных генов, имеющих дискретное фенотипическое проявление. Каждому признаку соответствует вектор определенного направления с длиной, равной частоте встречаемости данного признака. Векторы проводятся из центра круга, радиус которого равен 100 (соответствует 100% встречаемости признака), углы между смежными векторами равны. При соединении концов векторов признаков линией формируется контур полигона, который имеет сходную конфигурацию у групп с близкими частотами встречаемости признаков, но различную при несходстве частот. Полигоны А.С. Серебровского как геометрические фигуры обладают определенной формой. Если объекты или выборки сходны по признакам, то и полигоны будут сходны по форме. Вершины полигона легко «гомологизируются», так как для каждого признака задано определенное направление вектора, поэтому пригодны для расстановки ландмарок. Число и направление векторов, соответствующих изучаемым признакам, должно быть одинаковым у всех сравниваемых объектов. Это дает возможность сравнивать полигоны методами геометрической морфометрии. Следуя принципу построения полигона А.С. Серебровского можно визуализировать матрицы данных, характеризующие проявление гомологичных фенов неметрических признаков. А.Г. Васильев и И.А. Васильева (Васильев и др., 2018) предложили называть такие полигоны фенограммами или астеронами. Фенограммы могут быть представлены и в виде гистограмм, где признакам соответствуют вертикальные линии, но астероны более компактны, поэтому работать с ними обычно удобнее.
Метод фенограмметрии успешно апробирован авторами на разных видах растений и животных, в частности, на примере анализа встречаемости гомологичных фенов неметрических признаков черепа полевок рода Microtus (рис. 1).
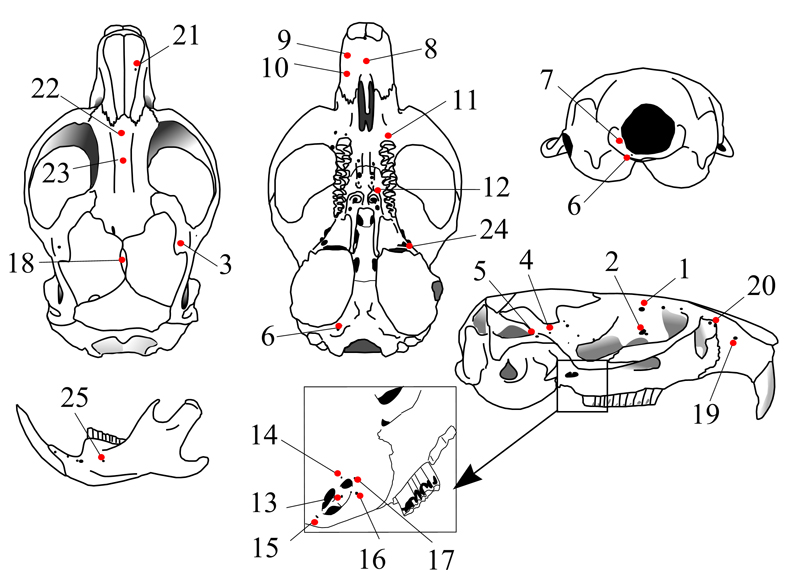
Рисунок 1 – Размещение 25 фенов неметрических пороговых признаков на осевом черепе и нижней челюсти восточноевропейской полевки (Microtus rossiaemeridionalis)
С помощью фенограммы можно визуализировать композицию проявившихся признаков у отдельной особи (рис. 2а) или частоты встречаемости признаков в выборке (рис. 2б). В первом случае фенограмма строится по матрице бинарных данных: если фен не проявился, конец соответствующего ему вектора окажется на внутренней окружности, а если проявился – на внешней. При визуализации частот встречаемости проявления фенов в выборке получается собственно полигон А.С. Серебровского – длины векторов равны частотам встречаемости соответствующих им признаков. Фенограммы можно обрабатывать стандартными методами геометрической морфометрии и статистики (рис.3).
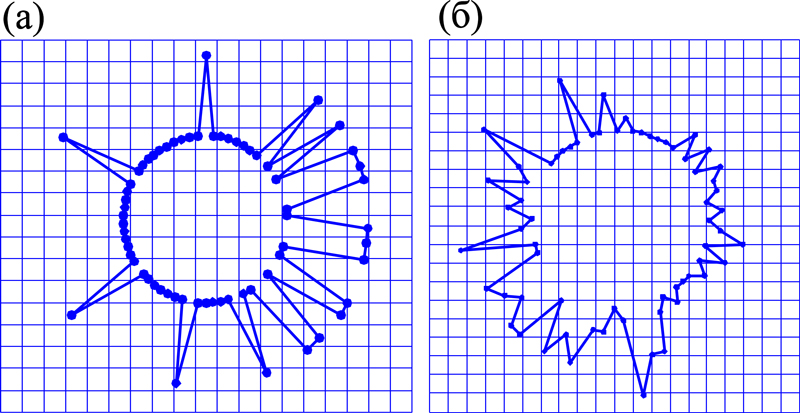
Рисунок 2 – Фенограммы, характеризующие (а) индивидуальное проявление и (б) частоты встречаемости фенов гомологичных неметрических признаков черепа обыкновенной полевки (Microtus arvalis)
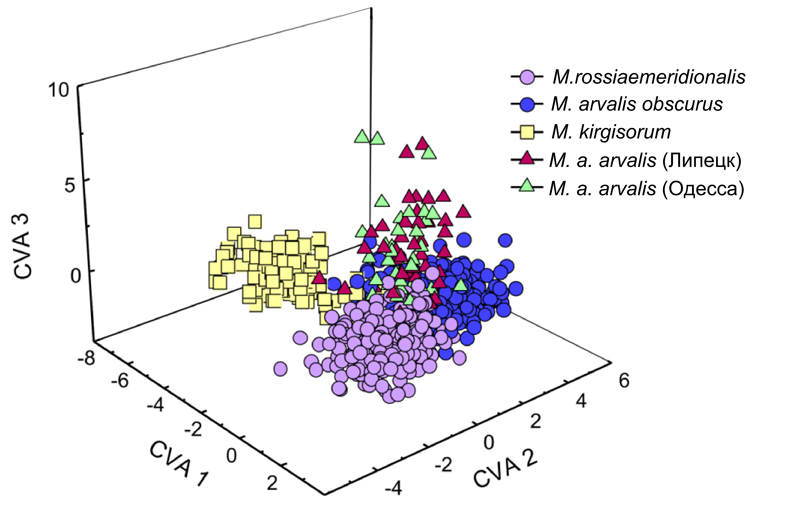
Рисунок 3 – Результаты канонического анализа фенограмм, построенных по 25 фенам пороговых неметрических признаков осевого черепа и нижней челюсти криптических видов и внутривидовых форм серых полевок рода Microtus
Предложенный подход универсален, применение методов геометрической морфометрии для анализа качественных признаков открывает новые возможности для решения задач таксономии, популяционной фенетики, феногенетики, популяционной и эволюционной экологии в плане визуализации и статистической обработки результатов.
